Concentrics.org

The conception

Phi 1.618, the numerical relationship in the Fibonacci sequence, was a fascination and an inspiration to me. I had a desire to create a new geometric expression of the sequence and chose the structural purity of the circle as my starting point. If the number 1 was represented by the centre circle, how would each subsequent number in the sequence be represented. I came upon the idea of using a ring of tangent circles or what I later learned to be “closed annular Steiner chains”. Each ring containing the same number of circles as the corresponding number in the sequence.

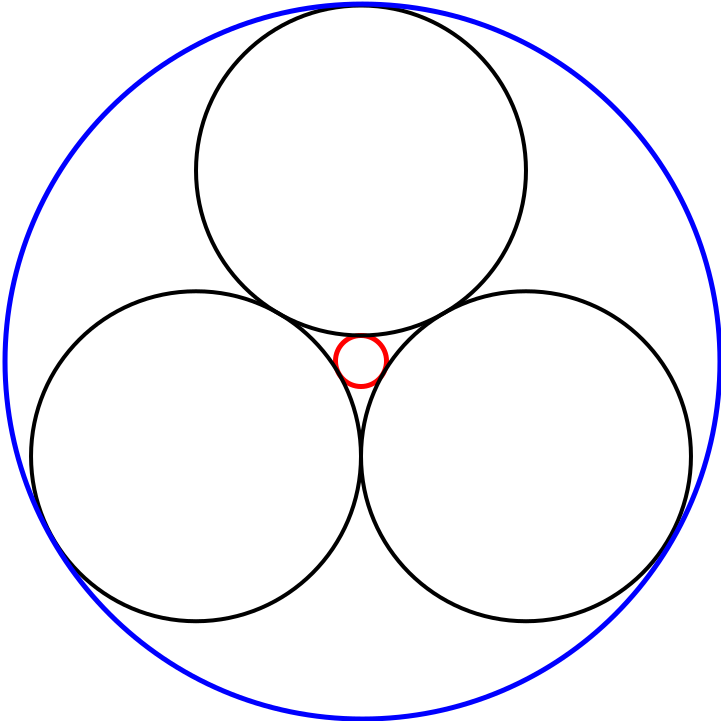
Number 2

As you can see in the image above, 3 is the minimum number of circles that can form a ring. This is why the number 2 is ignored in the visualiser. Therefore in the Fibonacci sequence, instead of 1,1,2,3,5,8,13… we use 1,3,5,8,13... simply missing out the 2 which has no effect on the remaining render.

The first visualisation

On an architectural CAD program, remembering SOH CAH TOA (a way of remembering how to compute the sine, cosine, and tangent of an angle), I constructed concentrically outwards from the previous ring a new Steiner chain. After 3 came 5 then 8 and 13 circles. With each ring the circle diameters increasing in size from the previous. Then with 21 came the first surprise, the diameter of these circles had decreased in size from the previous ring and continued to do so. On every subsequent ring the circle diameters reduced into infinity.

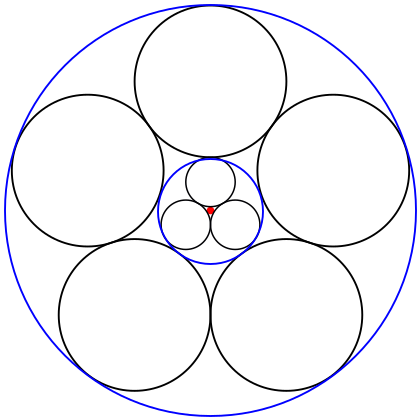
In the first completed nine ring construction of what I then called a Fibonacci Mandala, a myriad of features were revealed. This amazed me and lead me to wonder what other number sequences would reveal. Wishing to avoid the laborious geometric calculations that were previously involved, this web page was conceived and Concentrics.org was born. Now everyone can be amazed by the revelations of any appropriate number sequence. The Prime, Triangular and Tetrahedral ; the Square and Cubed; Arithmetic and Geometric, each having distinctly different features that act as an infographic of the maths that created them.

Preliminary observations

From the centre moving outwards the radii of circles can be seen to increase and decrease. The Fibonacci Concentric converges to an infinitely small radii diminishing at the rate of 0.618. Whilst the Prime Concentric is divergent to around hundred rings at which point the radii begin to reduce in diameter. This data is displayed on a graph below the main graphic. Visualisations such as the Prime, Triangular and Square have only one radial spoke, but concentric circles formed by multiplying the powers of 2 and 3 etc. have many. The spokes of the Fibonacci Concentric align to Fibonacci numbers in the individual ring chains. I look forward to the maths community investigating and exploring these and other features.

Visualise your own number sequence

On the Custom page your own inputs can be visualised and pre-set sequences can be edited. Start by entering a 0, or a 1, making sure all following numbers are whole numbers greater than 2. Ensure to separate all the numbers in your sequence with a comma. The numerals 0,1 & 2 will be ignored thereafter.

I hope fun can be had with the Steiner Concentrics Visualiser. Number sequences can be sourced on the web at oeis.org and there is no limit to one’s creativity.

C N Christopher BA Arch.
cliff@concentrics.org
Concentrics_org